Детерминизм (от лат. determino — определяю) — учение об объективной закономерной и причинной обусловленности всех явлений. В основе детерминирования лежит положение о существовании причинности, т. е. о такой связи явлений, при которой одно явление (причина) при вполне определенных условиях порождает другое (следствие). Детерминированный факторный анализ — методика исследования влияния факторов, связь которых с результативным показателем носит функциoнальный характер, т.е. результативный показатель может быть представлен в виде прoизведения, частногo или алгебраической суммы факторов.
В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
В детерминированных моделях предполагается, что результирующий показатель (или система таких показателей) функционально связан с показателями – факторами, значение результирующего показателя однозначно определяется значениями показателей факторов.
Модель баланса. Чем Вы заполняете свою жизнь?
Детерминированные модели типом могут быть четырех типов:
1) аддитивные: у = а + в, ; Y=Cумма Xi
2) мультипликативные: у = а * в, ; Y= П Xi
3) кратные: у = а / в;
4) смешанные: у = а * в + с, и т.д.
Детерминированные модели могут быть модифицированы. Как правило, это делается с целью разложения первоначальных показателей-факторов.
1) удлинение факторной модели: если У = Х1 / Х2, и Х1 = Х11 + Х12 + Х13 + …., тогда
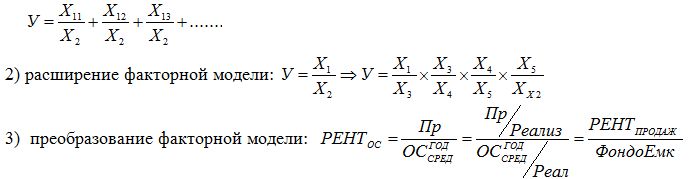
Виды детерминированных факторных моделей
Существуют следующие модели детерминированного анализа:
аддитивная модель, т. е. модель, в которую факторы входят в виде алгебраической суммы, в качестве примера можно привести модель товарного баланса: P=Зн+П-Зк-В,где Р — реализация; Зн — запасы на начало периода;П — поступление товаров; Зк- запасы на конец периода;В — прочее выбытие товаров;
мультипликативная модель, т. е. модель, в которую факторы входят в виде произведения; примером может служить простейшая двухфакторная модель: Р=Ч*ПТ,где Р — реализация;Ч — численность;
ПТ — производительность труда;
кратная модель, т. е. модель, представляющая собой отношение факторов, например:
где — фондовооруженность;ОС — стоимость основных средств;Ч — численность;
смешанная модель, т. е. модель, в которую факторы входят в различных комбинациях, например:
Pт=Р/ОС+Об ,где Р — реализация; Рт — рентабельность;ОС — стоимость основных средств;
Об — стоимость оборотных средств.
Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции можно применять такие детерминированные модели, как:
Презентация Динамической модели межотраслевого баланса в АСИ 15.11.2019
ВП=ЧР*ГВ ; ВП=ЧР*Д*ДВ; ВП=ЧР*Д*П*ЧВ
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов.
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения.
Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в качестве функции двух факторов: изменения суммы затрат (3) и объема выпуска продукции (VBП). Исходная модель этой факторной системы будет иметь вид:
Если общую сумму затрат (3) заменить отдельными их элементами, такими, как заработная плата (3П), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (HP) и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов:
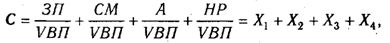
Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей.
Например, при анализе показателя рентабельности производства (R):
где П — сумма прибыли от реализации продукции; 3 — сумма затрат на производство и реализацию продукции. Если сумму затрат заменить на отдельные ее элементы, конечная модель в результате преобразования приобретет следующий вид:
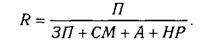
Метод расширения. Этот способ моделирования очень широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ = ВП /ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками (D), то получим следующую модель годовой выработки:
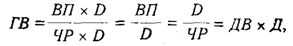
где ДВ — среднедневная выработка; Д — количество отработанных дней одним работником.
После введения показателя количества отработанных часов всеми работниками (Г) получим модель с новым набором факторов: среднечасовой выработки (ЧВ), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (Я):
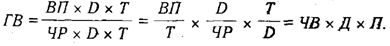
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Источник: studfile.net
Типы детерминированных моделей.
Все детерминированные модели можно свести к следующим типам:
- • аддитивные;
- • мультипликативные;
- • кратные;
- • смешанные.
Аддитивные модели представляют собой алгебраическую сумму показателей и имеют следующую математическую интерпретацию:

Они используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
Например, прибыль организации (77) представляет разность между выручкой от реализации продукции (В) и затратами на ее производство и реализации (3):

Себестоимость (С) продукции можно представить как сумму экономических элементов затрат:

где М3 — материальные затраты;
ЗП — заработная плата с отчислениями;
А — амортизация;
ПР — прочие расходы.
Мультипликативные модели представляет собой произведение факторов. В обобщенном виде она может быть представлена формулой:

Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.
Например, выручка от реализации (В) равна производной объема продукции (Q) и цены единицы продукции (Ц):
В = Q • Ц.
Кратные модели представляют собой отношение факторов и имеют следующий вид:

Она применяется тогда, когда результативный показатель получают делением одного факторного показателя на другой.
Например, для определения индекса цен на конкретную продукцию

Таким образом, цена на конкретный товар в отчетном периоде увеличилась на 20%.
Смешанные модели представляют собой комбинацию перечисленных моделей и могут быть описаны с помощью следующих выражений:

Примером смешанной модели является формула расчета рентабельности совокупных активов (Rca):

где В А — внеоборотные активы;
О А — оборотные активы.
Однако надо отметить, что не все математические выражения могут являться факторной моделью, если они не отражают причинно- следственную связь. Например, формула расчета производительности труда не является факторной моделью, так как объем реализации продукции не зависит от повышения производительности труда.
Первых три способа основываются на методе элиминирования, и именно они наиболее интересны для аналитика.
Элиминировать — значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Источник: studref.com
Детерминированная модель: определение. Основные типы факторных детерминированных моделей
Моделирование является одним из самых важных инструментов в современной жизни, когда хотят предвидеть будущее. И это не удивительно, ведь точность такого способа весьма велика. Давайте же в рамках данной статьи рассмотрим, что собой представляет детерминированная модель.
Общая информация

Детерминированные модели систем имеют ту особенность, что могут исследоваться аналитически, если они являются достаточно простыми. В противоположном случае при использовании значительного числа уравнений и переменных для этой цели могут задействоваться электронно-вычислительные машины. Причем помощь ЭВМ, как правило, сводится исключительно к их решению и нахождению ответов.
Из-за этого приходится менять системы уравнений и использовать другую дискретизацию. А это влёчет за собой повышенную опасность погрешности при расчетах. Все типы детерминированных моделей характеризуются тем, что знание параметров на определённом исследуемом интервале позволяет нам полностью определить динамику развития за границей известных показателей.
Особенности
Детерминированные математические модели не позволяют одновременно определять влияние множества факторов, а также не учитывают их взаимозаменяемость в системе обратных связей. На чем же выстраивается их функционал? Он базируется на математических закономерностях, которые описывают физико-химические процессы объекта. Благодаря этому достаточно точно предсказывается поведение системы.
Для строительства также используются обобщенные уравнения теплового и материального балансов, определяемых макрокинетикой процесса. Для большей точности прогнозирования детерминированная модель должна обладать максимально возможным количеством исходной информации про прошлое рассматриваемого объекта. Она может быть применена относительно тех технических задач, где допускается по той или иной причине пренебречь реально существующими флуктуациями значений параметров и результатами их измерения. Также одним из показаний к использованию является то, что случайные ошибки могут оказать несущественное влияние на конечный расчет системы уравнений.
Виды детерминированных моделей

Они могут быть не/периодическими. Оба вида могут быть непрерывным во времени. Также они представляются в виде последовательности дискретных импульсов. Описываться они могут с помощью изображения по Лапласу или благодаря интегралу Фурье.
Детерминированные факторные модели имеют определённые связи между входными и выходными параметрами процесса. Задаются модели посредством логических, дифференциальных и алгебраических уравнений (хотя могут использоваться и их решения, представленные как функция времени). Также в качестве основы для расчетов могут выступать экспериментальные данные, которые были получены в натуральных условиях или при ускоренных коррозионных испытаниях. Любая детерминированная модель предусматривает определённое усреднение характеристик системы.
Использование в экономике

Давайте рассмотрим практическое применение. Для этого подойдут детерминированные модели управления запасами. Следует отметить, что они формализованы в классе задач линейного программирования.
Так, для расчетов необходимо определить следующие показатели: затраты ресурсов и выпуск продукции с помощью различных способов производства, каждый из которых имеет свою интенсивность; переменные, описывающие все характеристики в происходящих процессах (в том числе и сырье с материалами). Всё должно быть проработано. Каждый отдельный ресурс, товар, услуга – всё это вносится в материальный баланс.
Также для полноты решений необходимо дать объективную оценку качества принимаемых решений. Таким образом, детерминированные экономические модели идеально подходят для описания процессов, от которых зависит начальное состояние системы. При работе с электронно-вычислительными машинами необходимо учитывать, что компьютеры могут работать только с фиксируемыми факторами.
Построение моделей
По способу представления основных параметров происходящих технологических процессов можно разделить два типа:
- Аппроксимационные модели. В них отдельные производственные единицы представлены как совокупность фиксированных векторов граничных вариантов их функционирования.
- Модели с переменными параметрами. В данном случае устанавливаются определённые диапазоны варьирования, и для соответствия векторам граничных вариантов вводятся дополнительные уравнения.
Эти детерминированные факторные модели позволят применяющему их человеку определить влияние конкретных положений на отдельные характеристики. Но получить для кривых разделения расчетные выражения не получится. Если же будет просчитываться динамическая оптимизация непрерывных производств, то не следует учитывать вероятностную природу информации о том, как протекают технологические процессы.
Факторное моделирование

Отсылки к этому можно было увидеть на протяжении всей статьи, но что это такое, мы пока не обсуждали. Факторное моделирование подразумевает, что выделяются основные положения, для которых необходимо количественное сопоставление. Для выполнения поставленных целей исследованием производят преобразование формы.
Если жестко детерминированная модель имеет больше двух факторов, то она называется многофакторной. Ее анализ может осуществляться посредством различных приёмов. В качестве примера приведем математическую статистику. В этом случае она рассматривает поставленные задачи с точки зрения заранее установленных и проработанных априорных моделей. Выбор среди них осуществляется по содержательному представлению.
Для качественного построения модели необходимо использовать теоретические и экспериментальные исследования сущности технологического процесса и его причинно-следственных связей. Именно в этом и заключается главное преимущество рассматриваемых нами субъектов. Модели детерминированного факторного анализа позволяют осуществлять точное прогнозирование во многих сферах нашей жизни. Благодаря их качественным параметрам и универсальности они и получили такое широкое распространение.
Кибернетические детерминированные модели

Они представляют для нас интерес благодаря основанным на анализе переходным процессам, которые возникают при любых, даже самых ничтожных изменениях агрессивных свойств внешней среды. Для простоты и быстроты расчетов существующее положение дел заменяется упрощенной моделью. Важным является то, чтобы она удовлетворяла всем основным запросам.
От единства всех необходимых параметров зависит работоспособность системы автоматического управления и эффективность принимаемых ею решений. При этом необходимо решить такую задачу: чем больше будет собрано информации, тем выше вероятность ошибки и значительнее срок обработки. Но если ограничить сбор своих данных, то можно рассчитывать на менее надёжный результат. Поэтому необходимо найти золотую середину, которая позволит получить информацию достаточной точности, и одновременно это не будет излишне усложнено лишними элементами.
Мультипликативная детерминированная модель
Она строится посредством разделения факторов на их множество. В качестве примера можно рассмотреть процесс формирования объема производимой продукции (ПП). Итак, для этого необходимо иметь рабочую силу (РС), материалы (М) и энергию (Э). В таком случае фактор ПП можно разбить на множество (РС;М;Э).
Такой вариант отображает мультипликативный вид факторной системы и возможность её разделения. В этом случае можно использовать такие методы преобразования: расширение, формальное разложение и удлинение. Первый вариант нашел широкое применение в анализе. Он может использоваться для того, чтобы высчитать эффективность деятельности работника, и так далее.
При удлинении одно значение заменяется другими факторами. Но в конечном итоге должно получиться то же самое число. Пример удлинения был рассмотрен нами выше. Осталось только формальное разложение. Оно предусматривает использование удлинения знаменателя исходной факторной модели благодаря замене одного или нескольких параметров.
Рассмотрим такой пример: мы рассчитываем рентабельность производства. Для этого сумма прибыли делится на размер затрат. При мультипликации вместо единого значения делим на просуммированные траты на материал, персонал, налоги и так далее.
Вероятности
О, если бы всё шло именно так, как задумано! Но такое бывает редко. Поэтому на практике часто вместе используются детерминированные и вероятностные модели. Что можно сказать про последние? Их особенность в том, что они учитывают ещё и различные вероятности. Возьмем, к примеру, следующее. Есть два государства. Отношения между ними очень плохи.
Третья сторона решает, инвестировать ли в предприятия одной из стран. Ведь если разгорится война, то прибыль очень пострадает. Или можно привести в пример построение завода в зоне с высокой сейсмической активностью. Здесь ведь действуют природные факторы, которые точно учесть нельзя, можно это сделать только приблизительно.
Заключение

Нами было рассмотрено, что собой представляют модели детерминированного анализа. Увы, но чтобы полноценно разобраться в них и уметь применять на практике, следует очень хорошо поучиться. Теоретические основы уже есть. Также в рамках статьи были представлены и отдельные простые примеры. Далее лучше идти по пути постепенного усложнения рабочего материала.
Можно немного упростить себе задачу и начать изучение программного обеспечения, которое может проводить соответствующее моделирование. Но каким бы выбор ни был, понимать основы и уметь дать ответ на вопросы о том, что, как и почему, всё же необходимо. Следует научиться для начала подбирать правильные входные данные и выбирать нужные действия. Тогда программы смогут успешно выполнять свои задачи.
Источник: fb.ru