Эта статья задумывалась как краткий ответ на вопрос N 40789, где обсуждались ошибки в функциях округления. Как сказал автор, «мне все равно что «бухгалтерское», что «арифметическое» — главное чтоб считало также как в Excel’е». Другими словами, возникла необходимость прояснить, чем отличается бухгалтерское округление от арифметического, какое из них реализовано в Excel’e — этом «гении чистой красоты», и почему некоторые Delphi-функции странным образом работают иначе.
Стоило копнуть эту тему поглубже, и новости повалили как из сказочного горшочка с кашей. Не претендуя на академическое раскрытие темы, поделюсь материалом, имеющимся на данный момент. Предлагаю следующий план:
- Очень кратко вспомним, почему вычисления на компьютере могут давать неожиданные результаты. Приведем некоторые ссылки.
- Подумаем, как можно с этим бороться. Для этого рассмотрим правила приближенных вычислений.
- Перейдем собственно к правилам округления. Особое внимание уделим так называемому «банковскому», или «бухгалтерскому» округлению, и покажем, зачем оно нужно, и какие еще способы округления существуют.
- Рассмотрим функции округления различных языков программирования, как встроенные, так и самописные. Покажем на примерах, что большинство из них, в том числе и встроенные функции Delphi, работает с ошибками. Укажем на правильную реализацию таких функций.
- В большом приложении к статье приведем полные результаты пятидесяти тестов функций округления разных языков, как встроенных, так и найденных на Круглом столе этого сайта, чтобы каждый мог, найдя в этом списке свою любимую функцию, увидеть, на каких значениях она, возможно, подвирает.
Итак, все мы в свое время обнаруживали, (а если нет — то вас еще ждет это волнующее открытие), что 0.1 в компьютере не равно 0.1. Читали статью «Неочевидные особенности вещественных чисел» Антона Григорьева, ужасались результатам сравнения и вычитания extended, погружались в дебри внутреннего представления чисел с плавающей запятой и размышляли о бесконечных цифровых хвостах. Интересующимся этой кухней порекомендуем классику — Дональд Кнут: «Искусство программирования», том 2, Глава 4. «Арифметика», где увлекательнейше описана история позиционных систем счисления, и в общем виде рассмотрены алгоритмы арифметики с плавающей запятой. Удачно дополняет ее статья Дэвида Голдберга «Что должен знать каждый ученый-компьютерщик о об арифметике с плавающей запятой». В ней приводятся некоторые теоремы, позволяющие оценить величину ошибок, возникающих в машинной арифметике, рассматриваются соответствующие IEEE-стандарты, и вопросы их реализации.
Возвращаясь из этих научных миров в реальную жизнь, приходится сделать неутешительный вывод: по сравнению со школьным курсом арифметики компьютеры считают неточно. Эта мысль достаточно тяжело укладывается в голове. Действительно, с первых уроков математики нам показывали рулетки, линейки, штангенциркули и микрометры, и говорили о том, что все измерения имеют погрешность.
Демонстрировали картинки с оптическими обманами и говорили о несовершенстве органов чувств. И в противовес этому превозносили саму математику, ее арифметические действия, как символ незыблемой правильности. Ведь еще Пифагор понял, что числа существуют независимо от нашего сознания, и логические рассуждения над ними переживут века. В народе это отразилось в поговорке «как дважды два — четыре» — то есть заведомо верно.
Чтобы снять с компьютера незаслуженный ореол научной святости, представим себе, что это всего лишь один из школьных измерительных приборов, со своими ограничениями и некоторым классом точности. А внутри него происходит вот что. Например, пусть нам нужно сложить два числа: 10 и 20. Берется школьная линейка и огурец.
Отрезается от огурца два кусочка: 10 и 20 мм длиной, складывается вдоль, и этой же кривоватой линейкой измеряется длина результата. Получаем ответ с некоторой погрешностью. Именно с такой степенью доверия нам придется относиться к результатам компьютерных вычислений с плавающей запятой.
Иногда приходится слышать, будто компьютеры считают приближенно. Но это совершенно не так. Для обсуждения этого вопроса срочно определимся с терминами.
Приближенные вычисления — давний и почтенный раздел математики. Он дает набор неких практических правил по обработке данных, полученных нашими несовершенными измерительными и вычислительными приборами. Именно следуя этим правилам, наша цивилизация вершила настоящие чудеса — строила храмы и мосты, предсказывала затмения, летала на фанерных аэропланах и керосиновых ракетах и стреляла из пушек за горизонт. И все это — заметьте — совершенно без помощи компьютеров. Что же это за столь замечательные правила?
Согласно Правилам Приближенных Вычислений (ППВ), каждому числу, полученному в результате измерений или вычислений, неотрывно сопутствует некая величина, характеризующая его точность. Эта величина может быть выражена абсолютной погрешностью, например (10 +/- 1); относительной погрешностью (10 +/- 10%); количеством значащих цифр, которое обычно выражается в записи (1.000); или записью числа в виде интервала возможных значений (99..101). Эти формы записи в общем-то эквивалентны, и могут быть получены одна из другой. Суть в том, что мы:
- Имеем на входе приближенные числа с известной погрешностью.
- Производим над ними арифметические действия как с точными числами
- На выходе имеем результат также с известной погрешностью.
Например, при сложении приближенных чисел достаточно просто сложить их абсолютные прогрешности. При умножении и делении — сложить относительные погрешности. Таким образом можно определить погрешность результата любой цепочки арифметических действий. Более подробно о ППВ можно прочитать в любом математическом справочнике.
Вернемся к нашим баранам — компьютерам. Что делают они?
- Имеют на входе некоторые числа.
- Вносят в них некоторую погрешность даже при присвоении переменным, как результат особенностей внутреннего представления.
- Производят над ними арифметические действия, внося некоторые погрешности как результат реализации вычислителя
- На выходе имеют неточный результат с неизвестной погрешностью.
Как видим, на алгоритмы ППВ похоже с точностью до наоборот.
Что же за странную задачу решает компьютер, и кому она такая нужна?
Подобный порядок вычислений имеет смысл лишь тогда, когда контроль точности результата ведется отдельно, либо заложен в саму задачу. В первом случае нам необходимо параллельно с формулами вычислений написать формулы вычисления погрешности. Иллюстрацией второго может быть решение некоего уравнения численными методами, когда берем результат в «артиллерийскую вилку», и итеративно приближаемся к нему с обеих сторон, прекращая вычисления при достижении шагом итерации некоего малого значения. Конечно, для решения учетно-бухгалтерских задач такие подходы выглядят экзотично. Но если вспомнить, что первые компьютеры использовались в основном для решения чисто научных либо военных задач (например, баллистики), то станет понятно, что другого от компьютеров тогда и не требовалось.
Ученые той поры привыкли к своенравной вычислительной технике, и учитывали это в соответствующих математических моделях. Представьте, например, баллистическую ракету. Десятиметровая бандура, сделанная из жести. Она не стоит, а скорее висит на захвате стартовой вышки, потому что жесткости у нее никакой — она играет как резиновая.
Включаются двигатели, захват отпускают, и представьте, что вы вертикально держите ее на кончике пальца, как карандаш. Карандаш норовит упасть, вы ловите отклонение и пододвигаете палец. А ракета, кроме того, ревет двигателями, норовит сложиться пополам, скрутиться по спирали, да и нужно ее не просто удержать, а запустить именно в заданную сторону.
Все это своенравие учитывается в математической модели устойчивости, выворачивается наизнанку и кладется в систему стабилизации и наведения — ящик между гироскопами и двигателями. А перед тем гоняем математическую модель ракеты на аналоговой ЭВМ — наборе операционных усилителей и деталюшек, изготовленных с точностью в лучшем случае 0.1%. И все работает.
Ну и скажите, имеет ли значение некоторая погрешность, если пыхтящую аналоговую ЭВМ заменить не совсем точной цифровой? Если исходная математика правильна и обратные связи модели отрабатываю верно, то все будет работать в любом случае. Поэтому не ругайте компьютеры — при правильном подходе из них можно извлечь немалую пользу.
Прошли времена железных людей, управляющих железными компьютерами. Теперь мы хотим считать на машинах килограммы, штуки, и конечно же деньги. И чтоб все сходилось до копеечки. А floating-point-вычислители-то остались прежними — пахнущими ракетной копотью и научной романтикой. И если мы хотим получить предсказуемые результаты и нести за них какую-то ответственность, то нам в наших программах придется вернуться к Правилам Приближенных Вычислений, и попытаться организовать их самостоятельно, не надеясь на компьютер, а используя его как вспомогательный инструмент.
Как мы уже говорили, ППВ позволяют знать погрешность результата на каждом этапе вычислений. Но для длинных цепочек трехэтажных формул прослеживание погрешности каждого этапа может оказаться делом нелегким, да и необходимо это сравнительно редко — в основном в научных задачах, где погрешность может оказаться соизмеримой с результатом. На практике пользуются упрощенными правилами, основанными на подсчете значащих цифр:
- При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков.
- При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих цифр.
- При возведении в квадрат или куб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближённое число ( последняя цифра квадрата и особенно куба при этом менее надежна, чем последняя цифра основания ).
- При увеличении квадратного и кубического корней в результате следует брать столько значащих цифр, сколько их имеет приближённое значение подкоренного числа (последняя цифра квадратного и особенно кубического корня при этом более надёжна, чем последняя цифра подкоренного числа).
- Во всех промежуточных результатах следует сохранять одной цифрой более, чем рекомендуют предыдущие правила. В окончательном результате эта «запасная» цифра отбрасывается.
- Если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру.
- Если данные можно брать с произвольной точностью, то для получения результата с K цифрами данные следует брать с таким числом цифр, какое даёт согласно правилам 1-4 (К+1) цифру в результате.
Здесь уместно привести высказывание выдающегося инженера-кораблестроителя академика Крылова, который говорил: «Лишняя вычисленная цифра есть ОШИБКА». Вопреки распространенному мнению, таскание хвостов незначащих цифр вместо их округления вовсе не повышает точности вычислений, а наоборот — может привести к накоплению ошибок в самых неожиданных местах.
Ну и кроме этого, речь идет об элементарной грамотности и аккуратности — при выводе результата 10,1230 лишние цифры могут создать впечатление их достоверности, скажем, до четвертого знака, в то время как исходные данные задавались плюс-минус лапоть. А это уже чревато рухнувшими мостами и взорванными реакторами. Недостоверные разряды следует округлять. Поэтому перейдем к фундаментальной операции приближенных вычислений — округлению.
Согласно школьного курса математики, при округлении чисел мы отбрасываем ненужные разряды, причем если первая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу. Будем называть этот способ «Арифметическим округлением».
Недоверчивый читатель, наверное, уже заподозрил, что сейчас пойдет речь и о других способах округления, и тянет руку с вопросом: а зачем, собственно? Чем не устраивает этот, столь родной и знакомый?
Проблема заключается в накоплении статистической погрешности при округлении большого количества чисел. Другими словами, многие задачи требуют, чтобы сумма столбика неокругленных значений была равна, или хотя бы близка сумме столбика округленных значений, а арифметическое округление приводит к серьезной и неизбежной ошибке, нарастающей с объемом данных. Причем это вовсе не связано с машинной арифметикой. Чтобы убедиться в этом, выключим компьютер, вооружимся счетами и карандашом, и решим такую задачу.
Контора заработала ровно миллион рублей, и поручила бухгалтеру разделить их на тысячу работников пропорционально коэффициенту трудового участия (КТУ). Тот выполнил арифметические действия и получил для каждого работника некоторое число Ni, с некоторым хвостиком дробных копеек. Убедился, что сумма всех Ni дает ровно миллион (мы опускаем проблемы неделимости нацело и бесконечных дробей — пусть хоть сегодня у нас все поделилось). Рассчитал сумму к выдаче — округлил каждое Ni до копеек, и подбил итог. И что же он видит?
Итог к выдаче составил что-то вроде один миллион рублей 50 копеек. А где ж эти 50 копеек взять? Он бы уже рад их и из своей получки добавить, да только проверяющие придут, и скажут — батюшки, да у вас бухгалтерия не пляшет — вот вы у нас теперь и попляшете. Плясать бухгалтеру вовсе не хотелось, поэтому вздохнул он и начал разбираться.
КТУ в конторе по старой советской традиции ставили с потолка, поэтому он достаточно хорошо подчинялся закону распределения случайных чисел. Соответственно, когда дело доходило до округления, то среди «первых отбрасываемых цифр» было примерно поровну нулей, единичек, двоек и всех остальных цифр.
Каждая операция округления вносила свою погрешность (разницу между первоначальным и округленным значением) в зависимости от отброшенного хвостика. При этом погрешности отброшенных единичек (-0.001) компенсировались погрешностями девяток (+0.001), двойки компенсировали восьмерки, и так далее, и лишь погрешности, вносимые при отбрасывании пятерок (+0.005), оставались нескомпенсированными, и накапливались. В среднем на тысяче человек встретилось 100 операций отбрасывания пятерки, каждая из которых дала погрешность пол-копейки. Отсюда и набежали злосчастные 50 копеек.
Вот фрагмент расчетной ведомости, демонстрирующий набегание одной копейки при раздаче суммы в 2000 руб.21 коп.:
Источник: www.interface.ru
Корректировка округления
Все формы бухгалтерской отчетности заполняются в тысячах или миллионах рублей. При заполнении форм необходимо, что бы выполнялись определенные математические соотношения, например, в балансе сумма показателей актива равнялась итого активу.
Возможна ситуация, когда, например, один показатель равен 1400 рублей, второй показатель 400 рублей, сумма показателей 1800 рублей, т.е. при переводе в тысячи рублей получается 1 тыс. руб., 0 и 2 тыс.руб. Т.о. в отчете итоговая сумма не будет равна сумме показателей.
При заполнении формы и переводе значений в тысячи, программа автоматически скорректирует показатели. Рассчитается разность между итоговой суммой и суммой показателей и эта разница прибавится к максимальному слагаемому.
В таблице приведен результат корректировки показателей при округлении до полных тысяч:
| В рублях | Округленное до полных тысяч | После корректировки | |
| Слагаемое 1 | 1 400 | 1 | 2 |
| Слагаемое 2 | 400 | 0 | 0 |
| Итоговая сумма | 1 800 | 2 | 2 |
Источник: www.erpandcrm.ru
Округление чисел в Microsoft Excel

При выполнении деления или работе с дробными числами, Excel производит округление. Это связано, прежде всего, с тем, что абсолютно точные дробные числа редко когда бывают нужны, но оперировать громоздким выражением с несколькими знаками после запятой не очень удобно. Кроме того, существуют числа, которые в принципе точно не округляются. В то же время, недостаточно точное округление может привести к грубым ошибкам в ситуациях, где требуется именно точность. К счастью, в программе имеется возможность пользователям самостоятельно устанавливать, как будут округляться числа.
Особенности округления чисел Excel
Все числа, с которыми работает Microsoft Excel, делятся на точные и приближенные. В памяти хранятся числа до 15 разряда, а отображаются до того разряда, который укажет сам пользователь. Все расчеты выполняются согласно хранимых в памяти, а не отображаемых на мониторе данных.
С помощью операции округления Эксель отбрасывает некоторое количество знаков после запятой. В нем применяется общепринятый способ округления, когда число меньше 5 округляется в меньшую сторону, а больше или равно 5 – в большую сторону.
Округление с помощью кнопок на ленте
Самый простой способ изменить округление — это выделить ячейку или группу ячеек и, находясь на вкладке «Главная», нажать на ленте на кнопку «Увеличить разрядность» или «Уменьшить разрядность». Обе кнопки располагаются в блоке инструментов «Число». Будет округляться только отображаемое число, но для вычислений при необходимости будут задействованы до 15 разрядов чисел.
При нажатии на кнопку «Увеличить разрядность» количество внесенных знаков после запятой увеличивается на один.
Кнопка «Уменьшить разрядность», соответственно, уменьшает на одну количество цифр после запятой.
Округление через формат ячеек
Есть возможность также выставить округление с помощью настроек формата ячеек. Для этого нужно выделить диапазон ячеек на листе, кликнуть правой кнопкой мыши и в появившемся меню выбрать пункт «Формат ячеек».
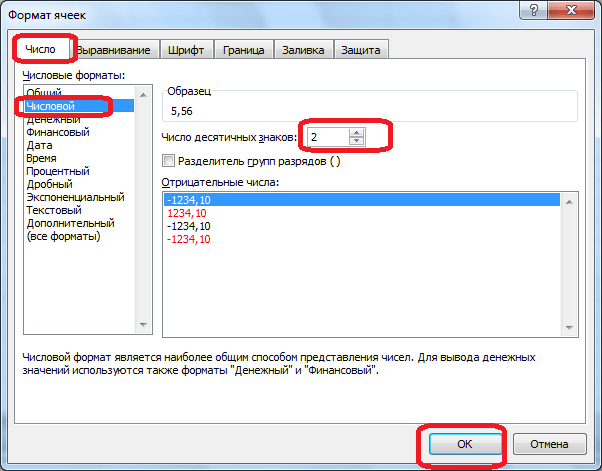
В открывшемся окне настроек формата ячеек следует перейти на вкладку «Число». Если формат данных указан не числовой, необходимо выставить именно его, иначе вы не сможете регулировать округление. В центральной части окна около надписи «Число десятичных знаков» просто укажите цифрой то количество знаков, которое желаете видеть при округлении. После этого примените изменения.
Установка точности расчетов
Если в предыдущих случаях устанавливаемые параметры влияли только на внешнее отображения данных, а при расчетах использовались более точные показатели (до 15 знака), то сейчас мы расскажем, как изменить саму точность расчетов.
- Перейдите на вкладку «Файл», оттуда — в раздел «Параметры».
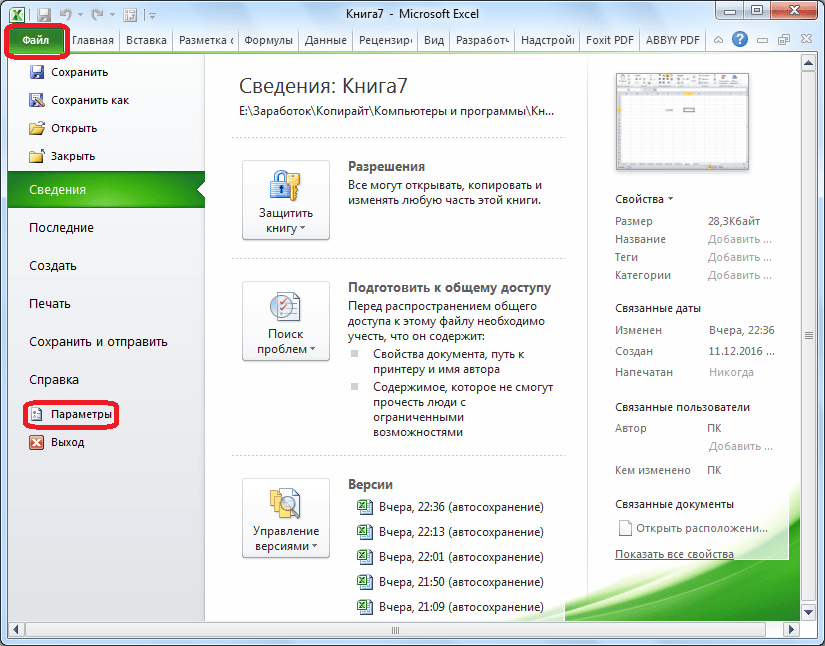
- Откроется окно параметров Excel. В этом окне зайдите в подраздел «Дополнительно». Отыщите блок настроек под названием «При пересчете этой книги». Настройки в этом блоке применяются не к одному листу, а к книге в целом, то есть ко всему файлу. Поставьте галочку напротив параметра «Задать точность как на экране» и нажмите «OK».
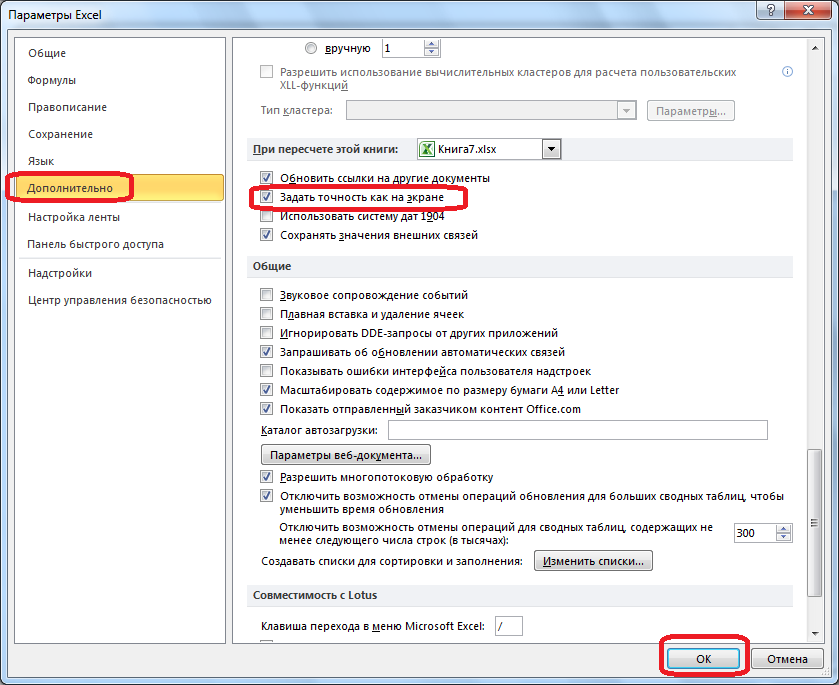
- Теперь при расчете данных будет учитываться отображаемая величина числа на экране, а не та, которая хранится в памяти Excel. Настройку же отображаемого числа можно провести любым из двух способов, о которых мы говорили выше.
Применение функций
Если же вы хотите изменить величину округления при расчете относительно одной или нескольких ячеек, но не хотите понижать точность расчетов в целом для документа, в этом случае лучше всего воспользоваться возможностями, которые предоставляет функция «ОКРУГЛ» и различные ее вариации, а также некоторые другие функции.
Среди основных функций, которые регулируют округление, следует выделить такие:
| ОКРУГЛ | Округляет до указанного числа десятичных знаков согласно общепринятым правилам округления |
| ОКРУГЛВВЕРХ | Округляет до ближайшего числа вверх по модулю |
| ОКРУГЛВНИЗ | Округляет до ближайшего числа вниз по модулю |
| ОКРУГЛТ | Округляет число с заданной точностью |
| ОКРВВЕРХ | Округляет число с заданной точностью вверх по модулю |
| ОКРВНИЗ | Округляет число вниз по модулю с заданной точностью |
| ОТБР | Округляет данные до целого числа |
| ЧЕТН | Округляет данные до ближайшего четного числа |
| НЕЧЕТН | Округляет данные до ближайшего нечетного числа |
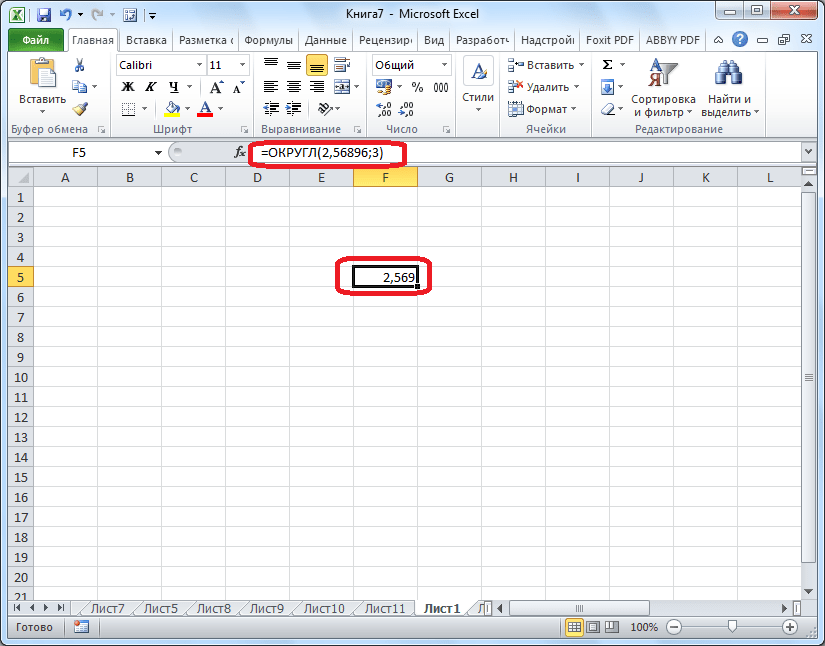
Для функций «ОКРУГЛ», «ОКРУГЛВВЕРХ» и «ОКРУГЛВНИЗ» используется следующий формат ввода: Наименование функции (число;число_разрядов) . То есть если вы, к примеру, хотите округлить число 2,56896 до трех разрядов, то применяете функцию «ОКРУГЛ(2,56896;3)». В итоге получается число 2,569.
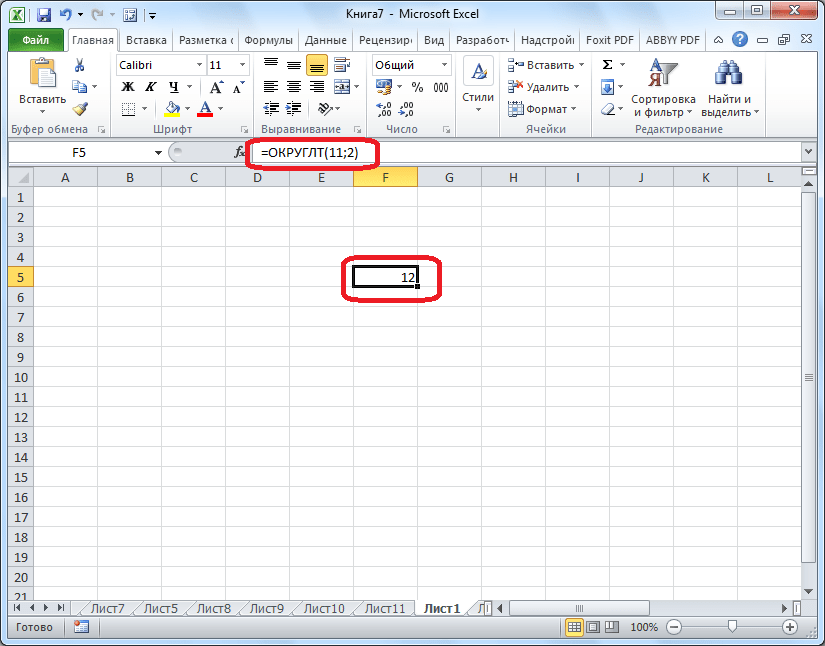
Для функций «ОКРУГЛТ», «ОКРВВЕРХ» и «ОКРВНИЗ» применяется такая формула округления: Наименование функции(число;точность) . Так, чтобы округлить цифру 11 до ближайшего числа, кратного 2, вводим функцию «ОКРУГЛТ(11;2)». На выходе получается результат 12.
Функции «ОТБР», «ЧЕТН» и «НЕЧЕТ» используют следующий формат: Наименование функции(число) . Для того чтобы округлить цифру 17 до ближайшего четного, применяем функцию «ЧЕТН(17)». Получаем результат 18.
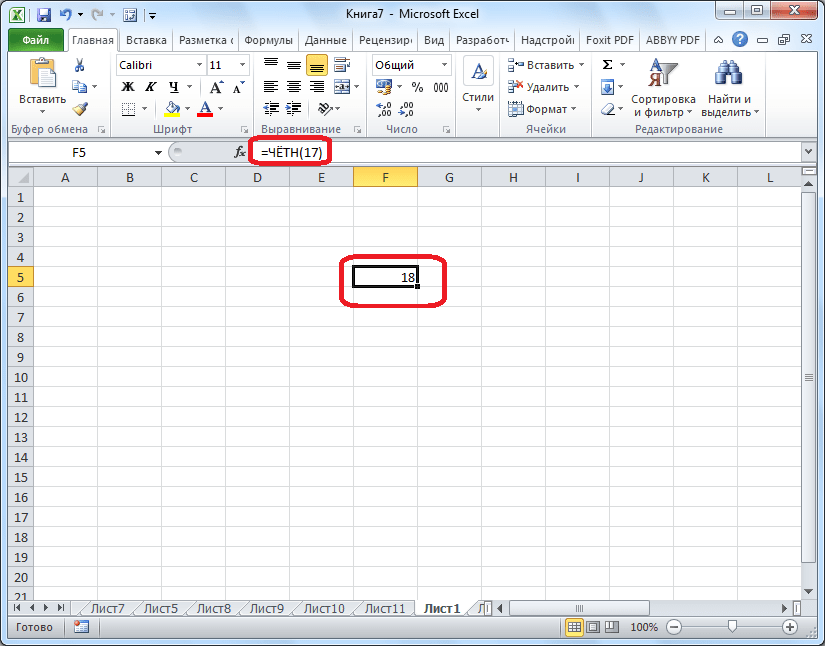
Функцию можно вводить, как в ячейку, так и в строку функций, предварительно выделив ту ячейку, в которой она будет находиться. Перед каждой функцией следует ставить знак «=».
Существует и несколько другой способ введения функций округления. Его особенно удобно использовать, когда есть таблица со значениями, которые нужно преобразовать в округленные числа в отдельном столбике.
- Переходим во вкладку «Формулы» и кликаем по кнопке «Математические». В открывшемся списке выбираем подходящую функцию, например, «ОКРУГЛ».
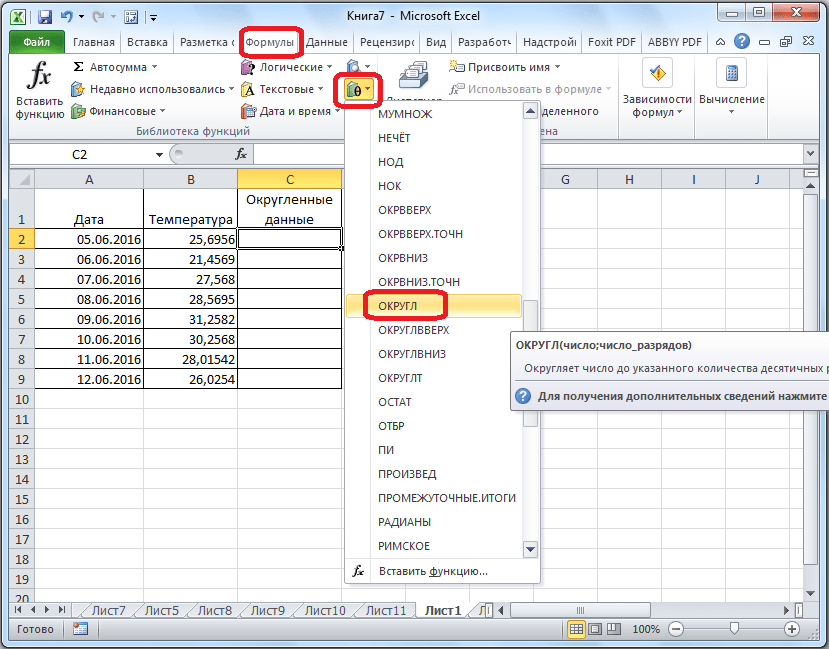
- После этого открывается окно аргументов функции. В поле «Число» можно ввести число вручную, но если мы хотим автоматически округлить данные всей таблицы, тогда кликаем по кнопке справа от окна введения данных.
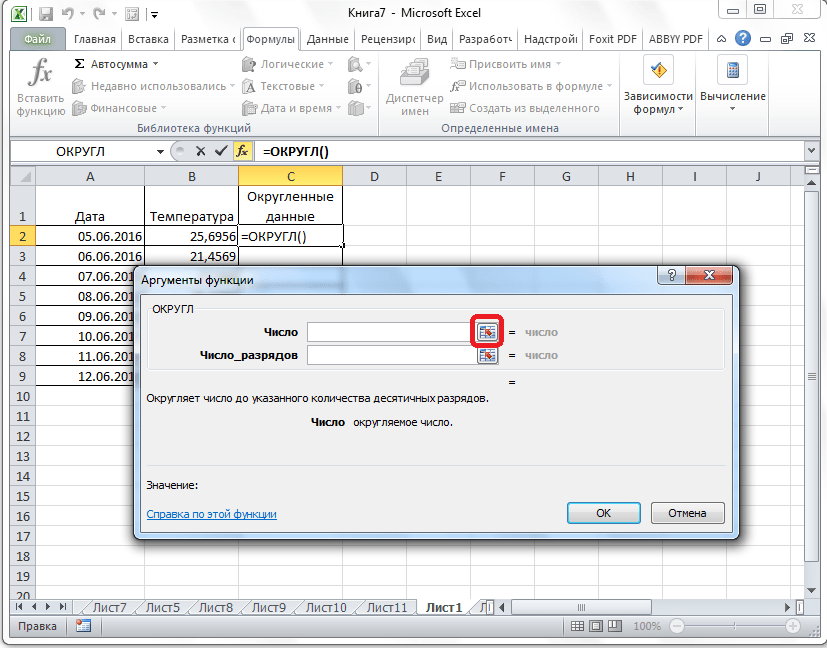
- Окно аргументов функции сворачивается. Теперь щелкнуте по самой верхней ячейке столбца, данные которого мы собираемся округлить. После того, как значение занесено в окно, жмем по кнопке справа от этого значения.
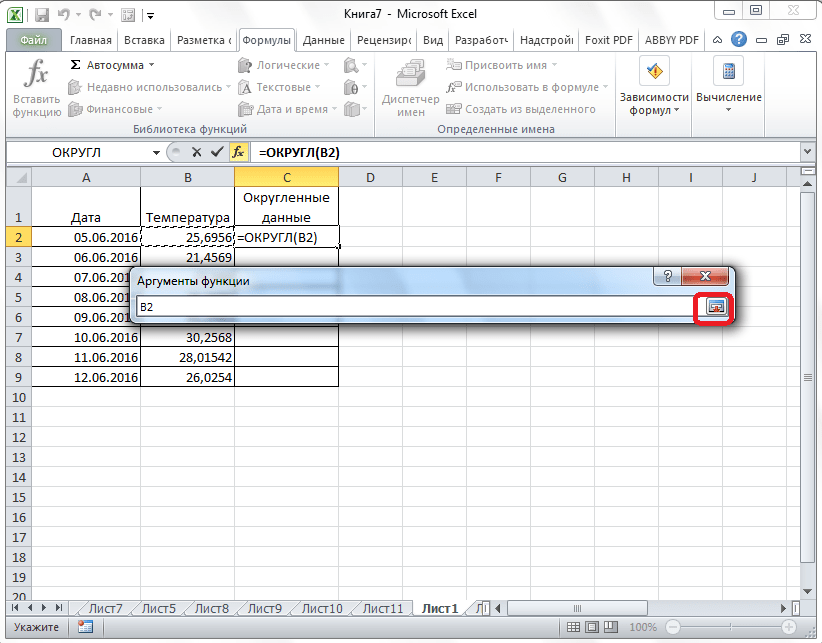
- Опять открывается окно аргументов функции. В поле «Число разрядов» записываем разрядность, до которой нам нужно сокращать дроби и применяем изменения.
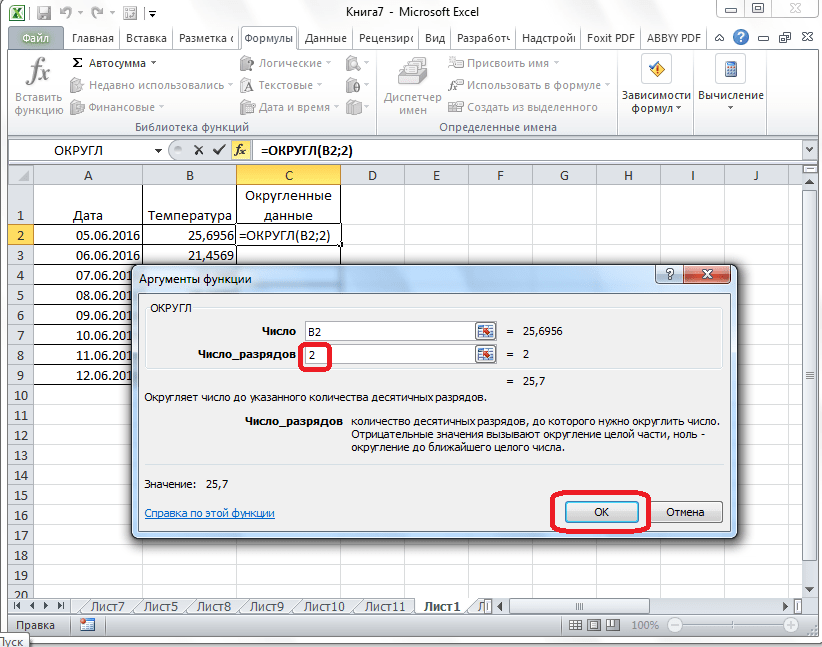
- Число округлилось. Чтобы таким же образом округлить и все другие данные нужного столбца, наводим курсор на нижний правый угол ячейки с округленным значением, жмем на левую кнопку мыши, и протягиваем ее вниз до конца таблицы.
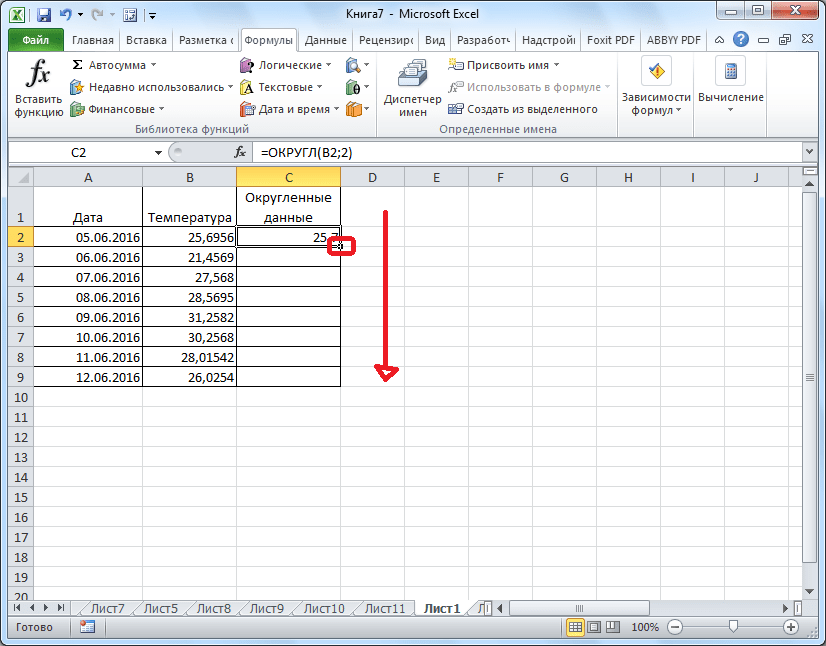
- Теперь все значения в столбце будут округлены.
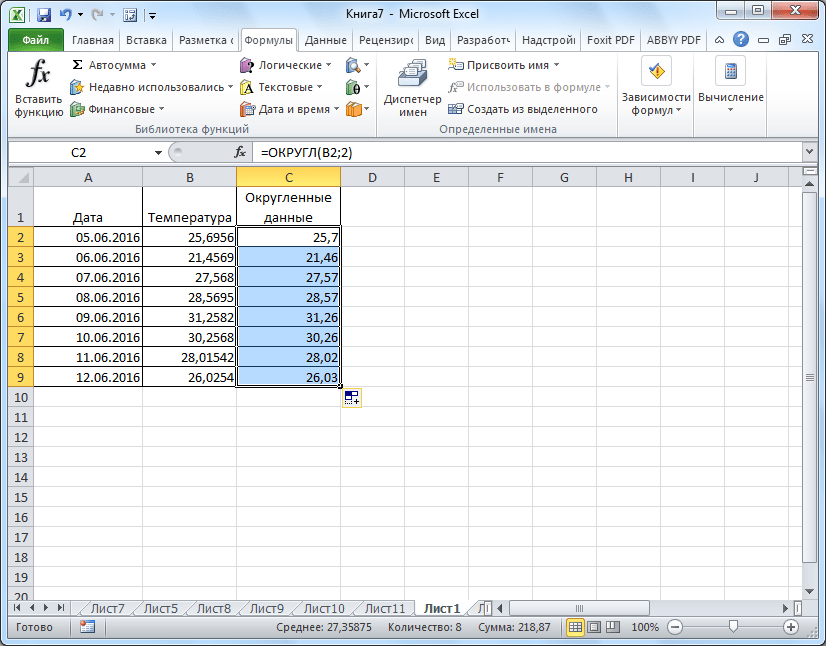
Как видим, существуют два основных способа округлить видимое отображение числа: с помощью кнопки на ленте и путем изменения параметров формата ячеек. Кроме того, можно изменить и округление реально рассчитываемых данных. Это также можно сделать по-разному: изменением настроек книги в целом или применением специальных функций. Выбор конкретного метода зависит от того, собираетесь ли вы применять подобный вид округления для всех данных в файле или только для определенного диапазона ячеек.
Источник: lumpics.ru